递归树
递归树指使用树的形式展现递归算法的实现,如下图为求解斐波那契数列的递归树:
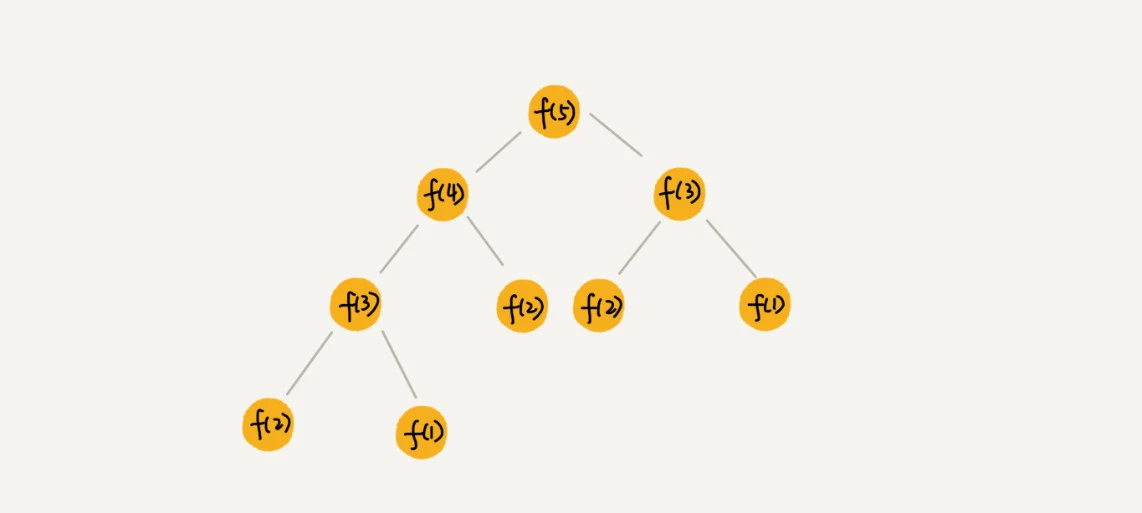
使用递归树可以更好地分析递归算法的时间复杂度。
分析上图中求斐波那契数列的时间复杂度:
f(n) 分解为f(n-1) 和 f(n-2)。从根节点走到叶子节点,每条路径长短不一,最长路径是 n,最段路径是 n / 2。
每次分解之后的合并操作只需要一次加法运算,把一次加法运算的时间消耗记为1。那么,第一层的总时间消耗为1(2的0次方),第二层为2的1次方,第三层3层为2的2次方……第 k 层的时间消耗为 2 的k-1次方。整个算法的总时间消耗就是每一层时间消耗之和。
如果将路径长度全部设为n,总和为2的n次方减1; 如果将路径长度全部设为 n / 2,总和为2的(n/2)次方减1。
因此,该算法的时间复杂度就介于O(2^n) 和 O(2^(n/2))之间。