Trie(字典树 前缀树)

前缀树是一种专门用于处理字符串匹配的树型数据结构，用来解决在一组字符i串集合中快速查找某个子符串的问题。

查询前缀树的时间复杂度是O(k)，其中k是字符串的长度。

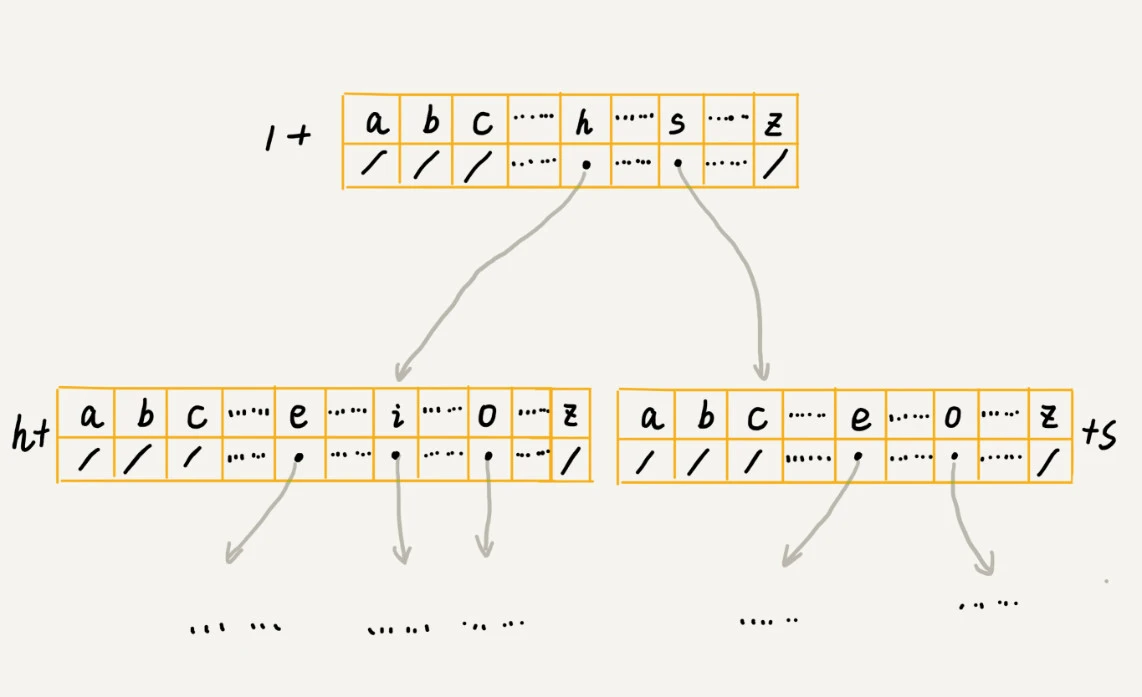
一个比较粗暴地实现trie树的方式，每个节点都使用一个数组来存放字符，假设字符串只有小写字母a-z，则每个节点都创建一个长度为26的数组，对应位置存放指向下一个节点的指针，其余位置置空：

代码实现(节点版)：

public class Trie {
  private TrieNode root = new TrieNode('/'); // 存储无意义字符
 
  // 往 Trie 树中插入一个字符串
  public void insert(char[] text) {
    TrieNode p = root;
    for (int i = 0; i < text.length; ++i) {
      int index = text[i] - 'a';
      if (p.children[index] == null) {
        TrieNode newNode = new TrieNode(text[i]);
        p.children[index] = newNode;
      }
      p = p.children[index];
    }
    p.isEndingChar = true;
  }
 
  // 在 Trie 树中查找一个字符串
  public boolean find(char[] pattern) {
    TrieNode p = root;
    for (int i = 0; i < pattern.length; ++i) {
      int index = pattern[i] - 'a';
      if (p.children[index] == null) {
        return false; // 不存在 pattern
      }
      p = p.children[index];
    }
    if (p.isEndingChar == false) return false; // 不能完全匹配，只是前缀
    else return true; // 找到 pattern
  }
 
  public class TrieNode {
    public char data;
    public TrieNode[] children = new TrieNode[26];
    public boolean isEndingChar = false;
    public TrieNode(char data) {
      this.data = data;
    }
  }
}
 

代码实现（二维数组）：

class Trie {  
    // 以下 static 成员独一份，被创建的多个 Trie 共用  
    static int N = 100009; // 直接设置为十万级  
    static int[][] trie = new int[N][26];  
    static int[] count = new int[N];  
    static int index = 0;  
  
    // 在构造方法中完成重置 static 成员数组的操作  
    // 这样做的目的是为减少 new 操作（无论有多少测试数据，上述 static 成员只会被 new 一次）  
    public Trie() {  
        for (int row = index; row >= 0; row--) {  
            Arrays.fill(trie[row], 0);  
        }  
        Arrays.fill(count, 0);  
        index = 0;  
    }  
      
    public void insert(String s) {  
        int p = 0;  
        for (int i = 0; i < s.length(); i++) {  
            int u = s.charAt(i) - 'a';  
            if (trie[p][u] == 0) trie[p][u] = ++index;  
            p = trie[p][u];  
        }  
        count[p]++;  
    }  
      
    public boolean search(String s) {  
        int p = 0;  
        for (int i = 0; i < s.length(); i++) {  
            int u = s.charAt(i) - 'a';  
            if (trie[p][u] == 0) return false;  
            p = trie[p][u];  
        }  
        return count[p] != 0;  
    }  
      
    public boolean startsWith(String s) {  
        int p = 0;  
        for (int i = 0; i < s.length(); i++) {  
            int u = s.charAt(i) - 'a';  
            if (trie[p][u] == 0) return false;  
            p = trie[p][u];  
        }  
        return true;  
    }  
}

使用「二维数组」的好处是写起来快，同时没有频繁  对象的开销。但是需要根据数据结构范围估算我们的「二维数组」应该开多少行。

坏处是使用的空间通常是方式的数倍，而且由于通常对行的估算会很大，导致使用的二维数组开得很大，如果这时候每次创建 对象时都去创建数组的话，会比较慢，而且当样例多的时候甚至会触发（因为每测试一个样例会创建一个对象）。

因此还有一个小技巧是将使用到的数组转为静态，然后利用  自增的特性在初始化  时执行清理工作 & 重置逻辑。